Bridge Beam Design [Post Tensioned]

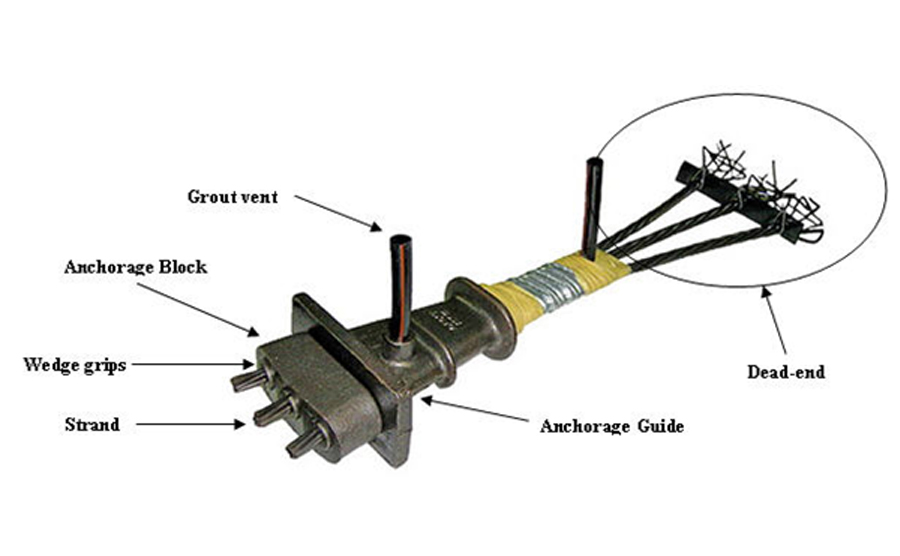
The Bridge beam is constructed mostly as posted tensioned or pre-tensioned beams. In addition to precast beams, concrete slabs on abutments, box culverts, box girders, suspension bridges are also constructed to accommodate passengers or vehicular movements.

The design of the post-tensioned bridge beam discussed in this article is in accordance with BS 8110 part 1.

In this article, we are discussing the ULS design (ULS bending moment capacity estimation)  of a post-tensioned bridge beam using the strain compatibility method.

Let’s discuss a little bit about the strain compatibility method.

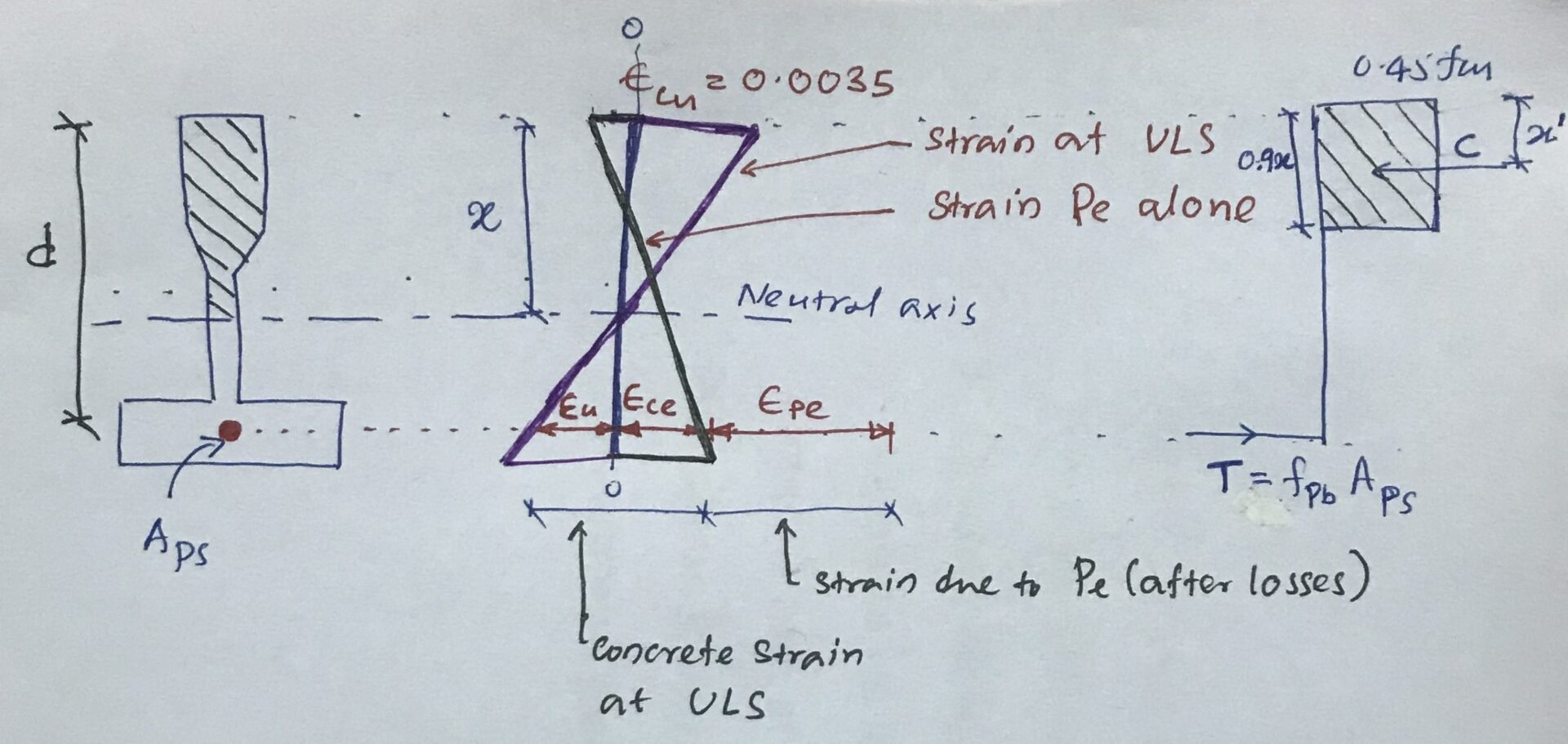
Ultimate limit state strain (ε_pb )in the selection at tension face is made from the following components.

1. Strain due to effective post-tension force( Pe) (after losses) – ε_pe
2. Strain-induced by the applied loading – ε_pa

Strain due to the prestressing Pe can be calculated as follows

ε_pe = P_e / [ A_ps.E_ps ]

where A_ps is the area of the tendons and E_ps is the steel elastic modulus.

During the prestressing, compression is below the neutral axis and the section is subjected to compression strains  ε_ce and ε_pe.

Here, ε_ceis the compressive strain in the section at the level of steel by the “Pe“.

Applied loads will first make this strain (ε_ce) zero, and then the steel tensile strain will be developed. The total tensile strain developed by ultimate limit state loading will be

ε_pa = ε_ce + ε_u

Further,

Reduction in concrete compressive strain = increase in steel tensile strain

This is because of the steel and the concrete in the same section. Concrete strain reduces and simultaneously steel strain increases. Both happen at once.

Here,

ε_ce  =  f_co /  E_c =  [P_e/E_c] [ 1/A + e²/I] 

ε_u = ε_cu [ d – x ] / x = 0.0035 [ d – x ] / x

The tensile strain of the steel can be expressed as

ε_pb = ε_u + ε_ce + ε_pe

We have to use an iterative process to calculate the neutral axis depth until compression force equals tension force (C = T)

Once we calculate the tensile strain (ε_pb ), calculate the bending capacity of the section from the following equation.

M_u = f_pb A_ps (d-d’)

The following steps are followed when the bending capacity of the bridge beam is calculated.

1. Assume a natural axis depth and calculate compression force (C = 0.45.fcu.A’_c)
2. Then calculate the tensile stress in the tendon.
3. For this, calculate the tensile strains in the tendons (ε_pb = ε_u + ε_ce + ε_pe)
4. And then find the steel strass from the stress-strain curve
5. Check whether the tensile force (T = f_pb A_ps) and the compression force is equal.
6. If not, repeat the calculate by changing the neutral axis depth until they are equal
7. After finding the neutral axis depth calculate the bending capacity of the section(M_u = f_pb A_ps (d-d’)).

Let’s study this with a worked example

Data for Bridge Beam Design 

• Span = 16m
• weight of the deck = 1 kN/m
• Imposed load = 4 kN/m
• Density of concrete 24 kN/m³
• Yield strength of tendons, f_pu = 1670 N/mm²
• Area of the tendons, A_ps = 882 mm²
• Concrete cube strength, f_cu = 40 N/mm²
• Area of the section, A = 121000 mm²
• Steel Elastic Modulus, E_ps = 205 kN/mm²
• Concrete Elastic Modulus, E_cu = 28 N/mm²
• Second Moment of the area of the section, I = 5.236×10⁹ mm⁴
• Prestressing Force, P_e = 744 kN

Calculate Design Moment

Desing load factors were taken from the BS 8110.

Area of the section =121000mm²

Selft weight of the beam = 121000 x 10^-6 x 24 = 2.9 kN/m

Design Load = 1.4 ( 2.9 + 1) + 1.6 x 4 = 11.86 kN/m

Design moment = wl²/8 = 11.86 x 16² / 8 = 379.52 kNm

Moment Capacity Check

Calculate the neutral axis depth

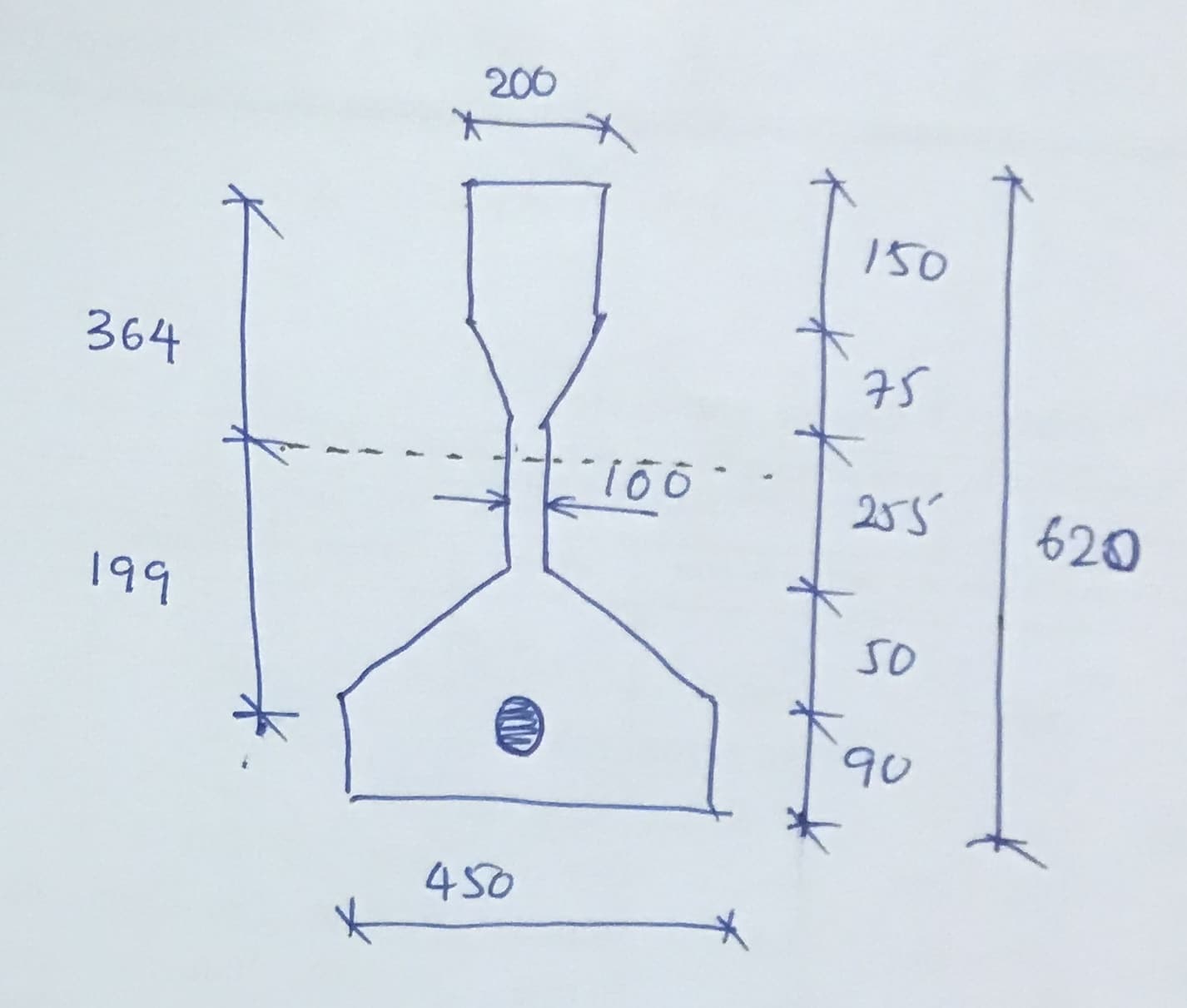
Assume neutral axis, x = 400mm from top extreme fibre

Heith of the compression stress block = 0.9 x = 0.9 x 400 = 360mm

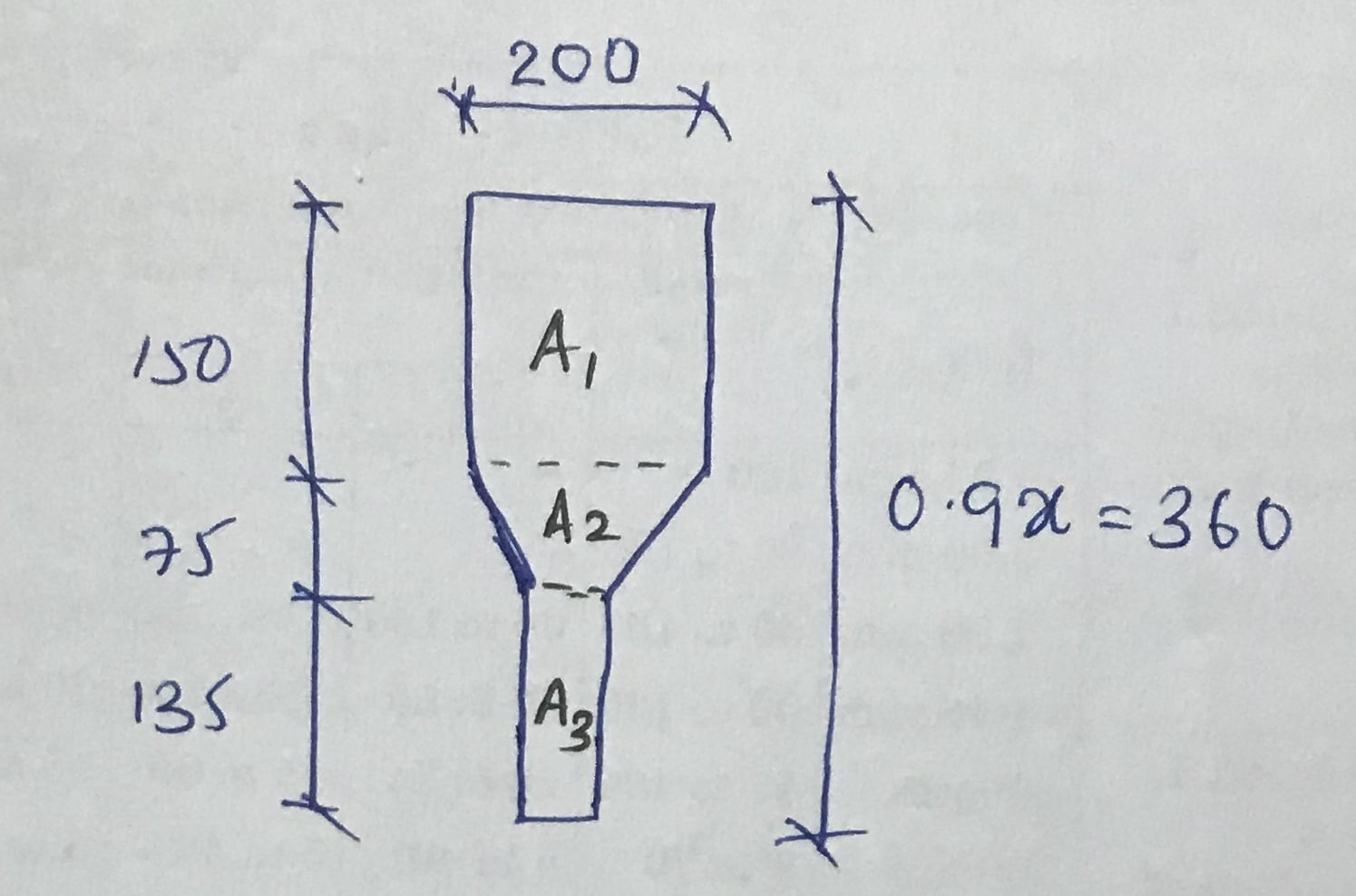
Area of the compression stress block, A’_c = A₁ + A₂ + A₃

A’_c = 150×200 + 0.5x(200+100)x75 + 135×100 = 54.75×10³ mm²

Compressive force

C = 0.45.fcu.A’_c

C = 0.45 x 40 x 54.75×10³ = 985.5×10³ N = 985.5 kN

Calculate Tension Force

T = f_pb A_ps

Firstly, we need to calculate the tensile stress (f_pb). Let’s use strain in the section.

ε_pb = ε_pe + ε_ce + ε_u = P_e/[A_ps.E_ps] + [P_e/E_c][ 1/A + e²/I] + 0.0035[d-x]/x

ε_pe = P_e/[A_ps.E_ps] = 744×10³ / (882 x 205×10³) = 4.11x 10^-3

ε_ce = [P_e/E_c][ 1/A + e²/I = [744×10³/28×10³][1/121000 + 199²/5.236×10⁹] = 0.42x 10^-3

ε_u = 0.0035[d-x]/x = 0.0035 x [(199+364) -400] / 400 = 1.43x 10^-3

ε_pb = 4.11x 10^-3 + 0.42x 10^-3 + 1.43x 10^-3 = 5.96x 10^-3

Strain in the tendon is 5.96x 10^-3  ≈ 0.006

From stress and strain diagram for prestressing tendons in BS 8110 Part 01, following infromation can be considered for the design

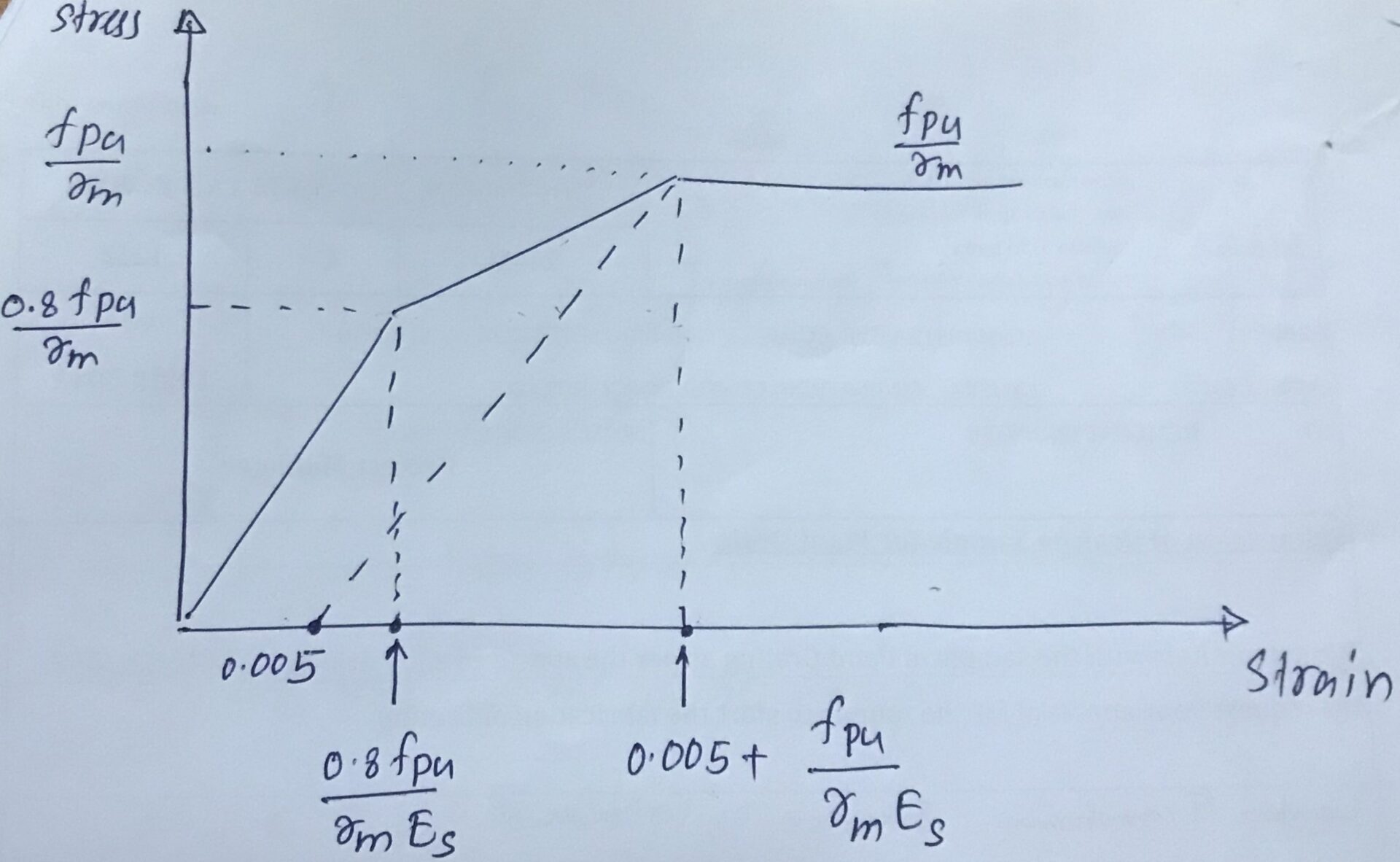
Follwoing information are available

• ϒ_m = 1.5
• f_pu = 1670 N/mm²
• E_ps = 205 kN/mm²

f_pu/γ_m = 1670 / 1.15 = 1452.2 N/mm²

0.8f_pu/γ_m = 1452.2 x 0.8 = 1161.7 N/mm²

f_pu/γ_mE_ps  = 1670 / (1.15 x 205×10³) = 0.0071

0.8f_pu/γ_mE_ps  = 0.0071 x 0.8 = 0.0057

Now values can be marked in the above figure as follows.

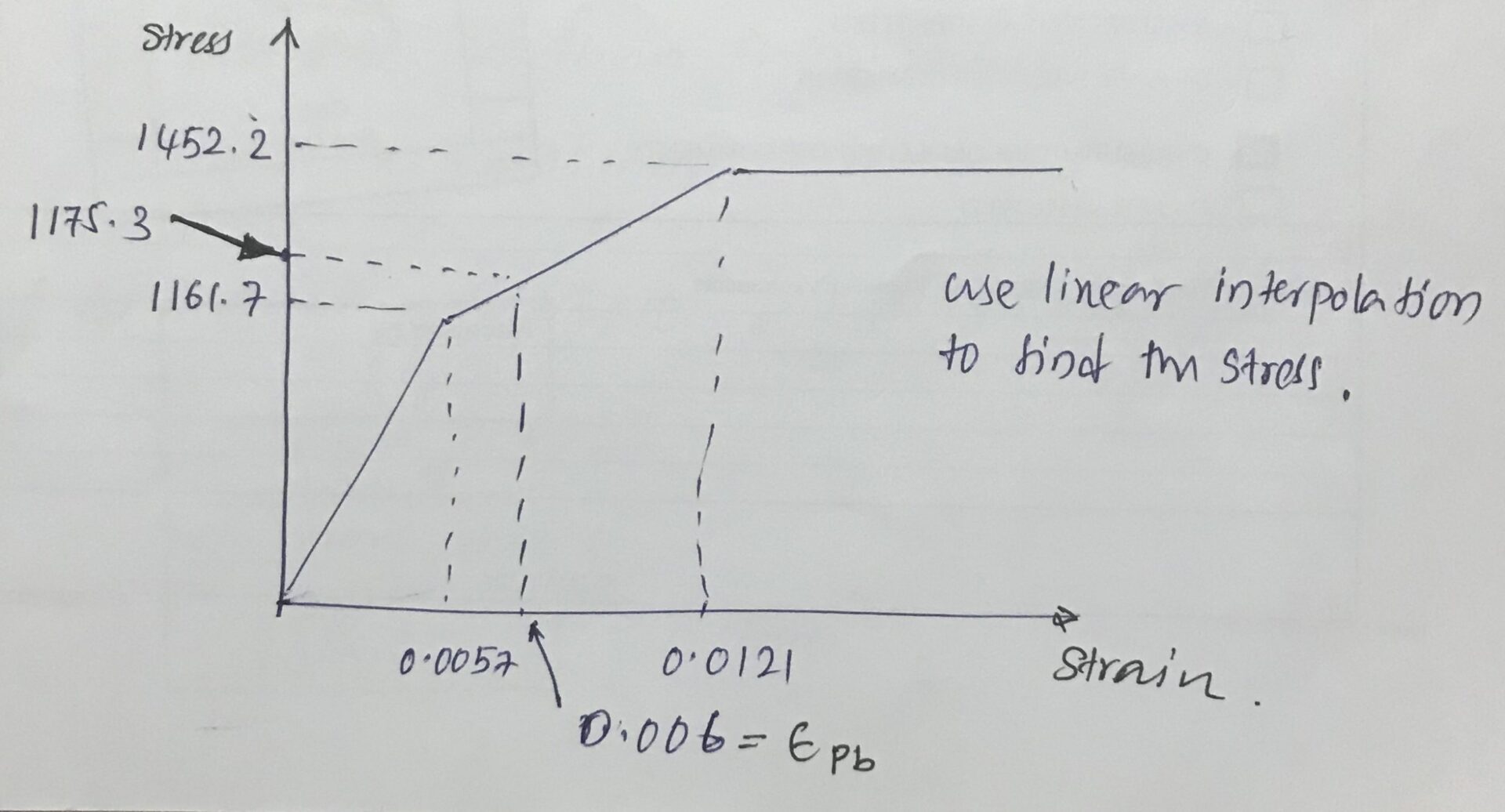
Using linear interpolation, we can find the stress in the tendons.

f_pb = 1175.3 N/mm²

Area of tendons, A_ps = 882 mm²

Now we can calculate the Tension force,

T = f_pb A_ps =  1175.3 x 882 = 1036.6×10³ N = 1036.6 kN

C = 985.5 kN

T ≠ C, the assumed neutral axis depth is not correct. We have to follow the same procedure until T = C.

We may have to do several iterations to get close to the correct neutral axis depth.

Firstly, we check the range for the neutral axis depth.

We can assume C = 1036.6 kN (tensile force) then check the depth

C = 0.45.fcu.A’_c

1036.6×10³ = 0.45 x 40 x A’_c

A’_c = 57588.9 mm²

57588.9 = 150×200 + 0.5x(200+100)x75 + (0.9x – 150 – 75 )x100

x = 431.54 mm

Thus, we can say that “x” should be less than this value.

Assume x = 425mm

ε_pb = 4.11x 10^-3 + 0.42x 10^-3 + 0.0035 x [(199+364) -425] / 425 = 0.0057

Following the similar procedure,  from above chart,

f_pb = 1161.7 N/mm²

T = f_pb A_ps =  1161.7 x 882 = 1024.6×10³ N = 1024.6 kN

C = 0.45.fcu.A’_c = 0.45 x 40 x [150×200 + 0.5x(200+100)x75 + 157.5×100} = 1026×10³ N = 1026 kN

Therefore, we can conclude that T ≈ C

Then consider, x = 425mm for calculating the bending capacity.

M_u = f_pb A_ps (d-d’)

Where d’ is the centroid of the compression stress block.

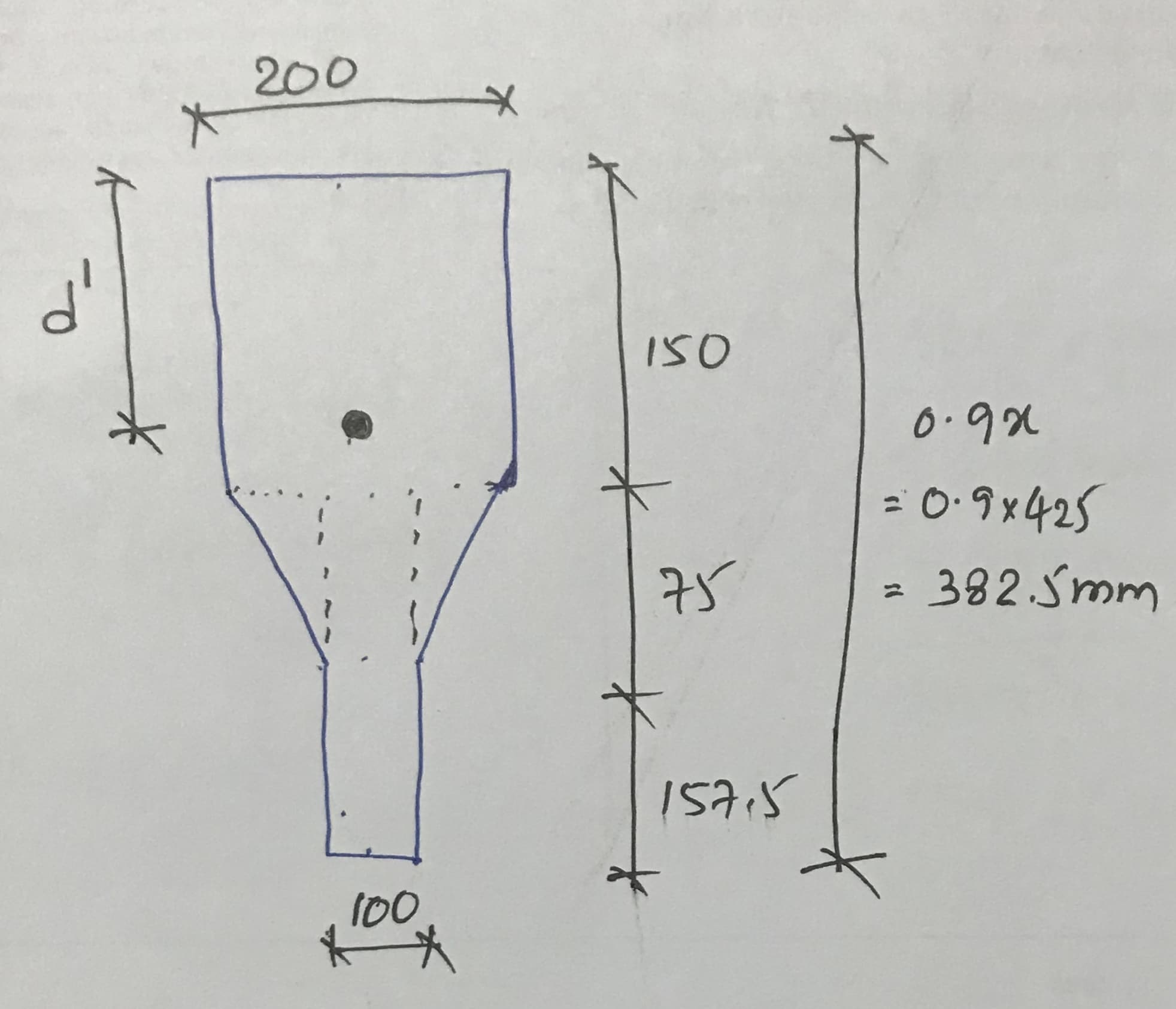
d’ can be calculated by taking the moment around an edge. Then the calculation is not included as it is a simple calculation.

d’ = 159.6mm

Let’s calculate the bending capacity.

M_u = f_pb A_ps (d-d’)

This equation can be written as

M_u = T (d-d’)

M_u= 1024.6 (563 -159.6) / 1000  = 413.3 kNm

The bending capacity is 413.3 kNm and the applied bending moment is 379.52 kNm. The section is ok for bending.

However, the section should be checked for the shear. You may refer to a separate article for the shear design of post-tension beams.

The article Bridge Design to BS 5400 could be referred to get more information on the bridge beam design theory.

Further reading on precast concrete the Wikipedia article prestressed concrete could be referred to.