Geometric nonlinearity is a fundamental concept in engineering that plays a crucial role in the analysis and design of structures. Unlike linear analysis, which assumes that structures behave linearly under loading, geometric nonlinearity considers the deformations caused by large displacements, rotations, and strains. In this article, we will explore the concept of geometric nonlinearity, its importance in engineering, its effects on structural behavior, and its various applications.
In engineering analysis, it is common to assume that structures respond linearly to external forces. However, in real-world scenarios, this assumption may not hold true when dealing with large deformations or highly flexible systems. Geometric nonlinearity takes into account the changes in geometry that occur as a result of these deformations, providing a more accurate representation of the structural response.
Understanding Geometric Nonlinearity
Geometric nonlinearity refers to the deviation from linearity in the geometry of a structure when subjected to significant loads or displacements. This deviation arises due to the large rotations, translations, and strains experienced by the structure. It is important to consider geometric nonlinearity when the displacements and rotations become comparable to the size of the structure or when the applied loads induce significant deformations.
Importance of Geometric Nonlinearity in Structural Engineering
Geometric nonlinearity is of paramount importance in engineering for several reasons.
Firstly, it allows engineers to accurately predict the behavior of structures under large deformations. Linear analysis fails to capture the nonlinear effects that can lead to unexpected or catastrophic failures. By considering geometric nonlinearity, engineers can assess the stability, strength, and overall performance of structures more reliably.
Secondly, geometric nonlinearity plays a crucial role in the design optimization process. Neglecting geometric nonlinearity can lead to over-conservative designs or structures that are prone to failure. By accounting for geometric nonlinearity, engineers can optimize the design, reduce material usage, and enhance the overall efficiency of the structure.
Effects of Geometric Nonlinearity
Geometric nonlinearity introduces several effects that significantly impact the behavior of structures. These effects include:
1. Large deformations and rotations:
Under geometric nonlinearity, structures can undergo substantial deformations and rotations. This can result in changes in stiffness, altered stress distributions, and potential instability.
2. Load redistribution:
Geometric nonlinearity can cause load redistribution within a structure. As deformations occur, forces and moments are redistributed, affecting the overall structural response. Further, inadequate capacity of the structural element resulted with the increase in the forces could cause structural failures.
3. Buckling and post-buckling behavior:
Geometric nonlinearity plays a significant role in the buckling and post-buckling behavior of structures. When the deformations of a structure become large, the assumption of small displacements and strains, which is inherent in linear analysis, is no longer valid. Geometric nonlinearity takes into account the changes in geometry that occur as a structure deforms, leading to nonlinear behavior.
Buckling refers to the sudden failure or collapse of a structure due to an unstable equilibrium. Geometric nonlinearity affects buckling behavior by introducing additional deformations and changes in shape as the structure reaches critical loads. In linear analysis, the buckling load is determined solely by the material and stiffness properties of the structure. However, in the presence of geometric nonlinearity, the critical load also depends on the initial shape and boundary conditions.
Post-buckling behavior refers to the response of a structure after it has buckled. Geometric nonlinearity influences post-buckling behavior by introducing large deformations and changes in stiffness. Following buckling, the structure undergoes a series of equilibrium configurations as it adapts to the new loading conditions. The post-buckling behavior can exhibit complex shapes, local deformations, and interactions between different modes of deformation.
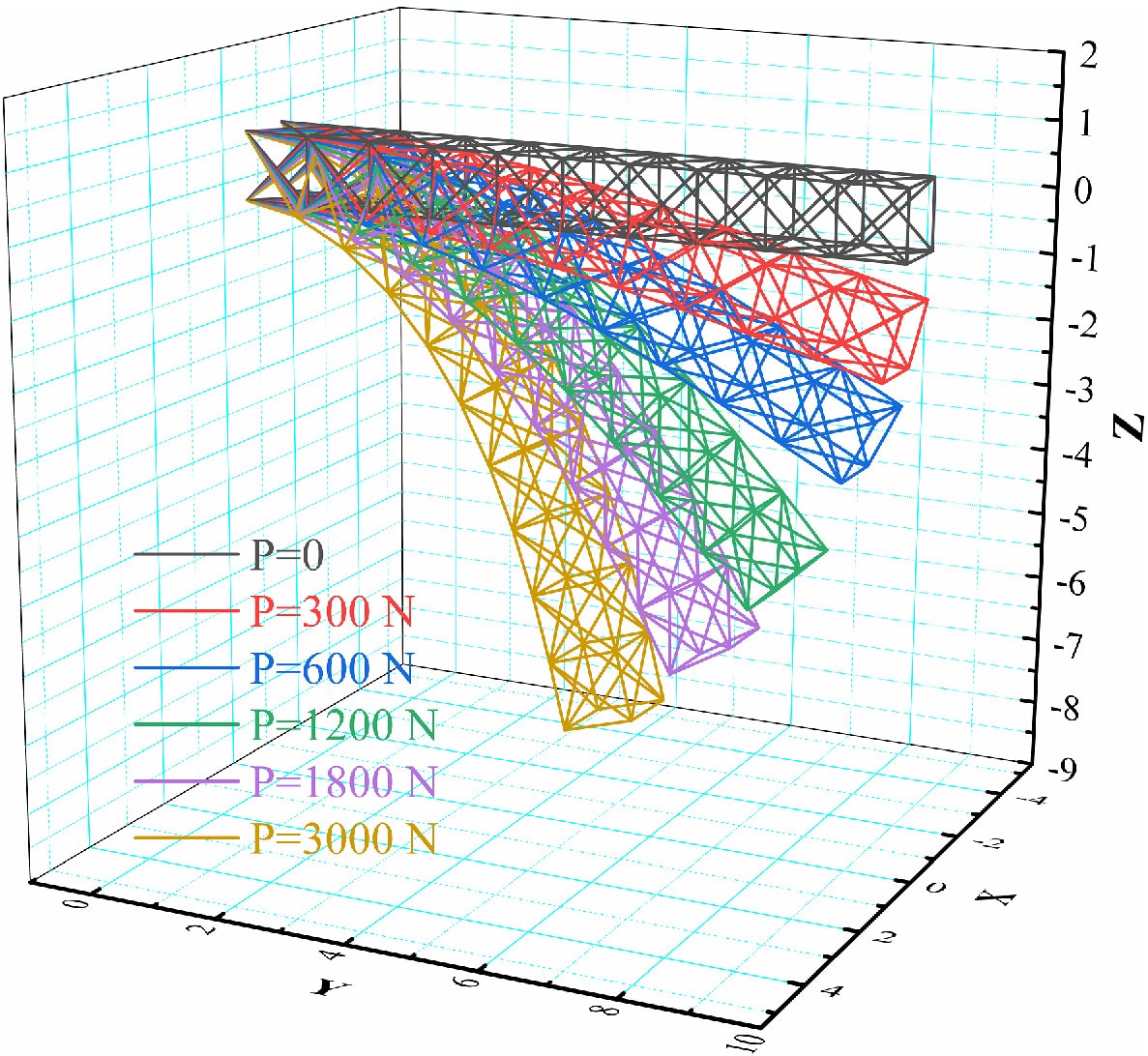
Mathematical Modeling of Geometric Nonlinearity
To analyze and predict the behavior of structures under geometric nonlinearity, mathematical models are employed. These models consider the nonlinear relationships between displacements, rotations, and applied loads. Finite element analysis (FEA) is a widely used technique for modeling geometric nonlinearity. FEA discretizes the structure into small elements, allowing for accurate representation of the complex geometry and nonlinear behavior.
Various constitutive models are used to describe the material response under geometric nonlinearity. These models consider factors such as strain-hardening, large deformations, and stress-strain relationships. Nonlinear equilibrium equations are solved iteratively to obtain the displacements, rotations, and internal forces that satisfy the equilibrium conditions.
Analysis Techniques for Geometric Nonlinear Problems
Analyzing geometric nonlinear problems requires specialized techniques beyond traditional linear analysis. Some commonly employed techniques include:
1. Incremental-iterative methods:
These methods divide the analysis into small increments and iteratively solve the equilibrium equations at each increment. The incremental approach ensures that the nonlinear effects are captured accurately.
2. Load or displacement control:
In geometric nonlinear analysis, the loading can be controlled in terms of applied forces or prescribed displacements. This allows for the exploration of different loading scenarios and the evaluation of the structure’s response under varying conditions.
3. Nonlinear buckling analysis:
Geometric nonlinearity significantly affects the buckling behavior of structures. Nonlinear buckling analysis identifies critical loads and corresponding modes of failure, providing insights into structural stability.
4. Dynamic analysis:
Geometric nonlinearity can have a substantial impact on the dynamic behavior of structures. Dynamic analysis techniques, such as modal analysis or time-history analysis, consider the effects of nonlinear behavior on natural frequencies, mode shapes, and dynamic response.
In conclusion, geometric nonlinearity is a crucial aspect of engineering analysis that accounts for the deformations and rotations occurring in structures under significant loads. It is important to understand and consider geometric nonlinearity to ensure accurate predictions of structural behavior, optimize designs.
Applications of Geometric Nonlinearity
Geometric nonlinearity finds applications in various fields of engineering. Some notable applications include:
1. Structural engineering:
Geometric nonlinearity is of utmost importance in structural engineering. It plays a significant role in analyzing and designing structures such as bridges, buildings, and aerospace components. Considering geometric nonlinearity helps ensure structural safety, stability, and performance under realistic loading conditions.
2. Mechanical engineering:
In mechanical engineering, geometric nonlinearity is essential for analyzing mechanisms, machine components, and mechanical systems. It aids in understanding the behavior of flexible bodies, joints, and linkages, leading to improved performance and reliability.
3. Material modeling:
Geometric nonlinearity is closely related to material behavior and deformation. It is used in material modeling to accurately represent nonlinear phenomena, such as plasticity, viscoelasticity, and hyperelasticity. Material models incorporating geometric nonlinearity enable more realistic simulations and predictions.
4. Computational fluid dynamics (CFD):
CFD simulations often require considering the effects of geometric nonlinearity, especially in fluid-structure interaction problems. Geometric nonlinearity influences the behavior of flexible structures in fluid flow, providing insights into the dynamics and stability of systems like offshore platforms, wind turbines, and aircraft wings.
5. Biomechanics:
Geometric nonlinearity plays a significant role in the analysis of biological structures, such as bones, soft tissues, and organs. It helps understand the deformation and response of these structures under various loading conditions, aiding in medical research, prosthetics design, and surgical simulations.
FAQ
What is the difference between linear and geometric nonlinear analysis?
Linear analysis assumes that structures behave linearly under loading, neglecting the effects of large deformations and rotations. Geometric nonlinear analysis considers the nonlinear relationships between displacements, rotations, and applied loads, providing a more accurate representation of structural behavior.
How does geometric nonlinearity affect structural stability?
Geometric nonlinearity can affect structural stability by inducing buckling, altering mode shapes, and redistributing forces and moments within the structure. Neglecting geometric nonlinearity can lead to underestimation of critical loads and potential structural failures.
Can geometric nonlinearity be ignored in engineering analysis?
In many engineering scenarios involving large deformations, rotations, or flexible structures, geometric nonlinearity cannot be ignored. Neglecting geometric nonlinearity may result in inaccurate predictions, compromised safety, and inefficient designs.
Are there any software tools available to handle geometric nonlinear problems?
Yes, there are several software tools available that can handle geometric nonlinear problems. These tools utilize advanced numerical methods and provide capabilities for modeling, simulation, and analysis of structures under geometric nonlinearity. Examples include Abaqus, ANSYS, and LS-DYNA.
What are some real-life examples where geometric nonlinearity plays a significant role?
Real-life examples where geometric nonlinearity is significant include the analysis of tall buildings subjected to wind and seismic loads, the design of curved bridges and arches, the simulation of flexible robotic manipulators, and the study of heart valve mechanics in biomedical engineering.


