Nonlinear analysis of structures is a powerful technique used in engineering to understand and predict the behavior of structures under complex loading conditions. Unlike linear analysis, which assumes structures behave linearly, nonlinear analysis considers the effects of large deformations, material nonlinearity, and contact interactions. In this article, we will explore the significance of nonlinear analysis, its various types, techniques used, challenges faced, applications, and future developments.
Structures are subjected to a wide range of forces and loads during their lifetime. Analyzing their behavior accurately is crucial to ensure their safety and optimize their design. Nonlinear analysis plays a vital role in this regard by accounting for the nonlinear responses exhibited by structures. It enables engineers to simulate real-world scenarios and obtain more realistic results.
Nonlinear analysis considers the effects of several factors, such as geometric nonlinearity, material nonlinearity, and contact interactions. By incorporating these complexities, engineers can gain insights into the structural response beyond the limitations of linear analysis.
Linear vs. Nonlinear Analysis
Linear analysis is a widely used method for predicting the behavior of structures under small deformations. It assumes that the relationship between the applied loads and the structural response remains linear throughout the loading process. While linear analysis provides reasonable approximations for many engineering problems, it has certain limitations.
Structures subjected to large deformations or nonlinear material behavior require a more sophisticated approach. Nonlinear analysis acknowledges that the structural response may deviate significantly from linearity, providing a more accurate representation of reality.
Types of Nonlinear Analysis
Nonlinear analysis can be classified into different types based on the factors being considered. The three primary types are geometric nonlinearity, material nonlinearity, and contact and frictional nonlinearity.
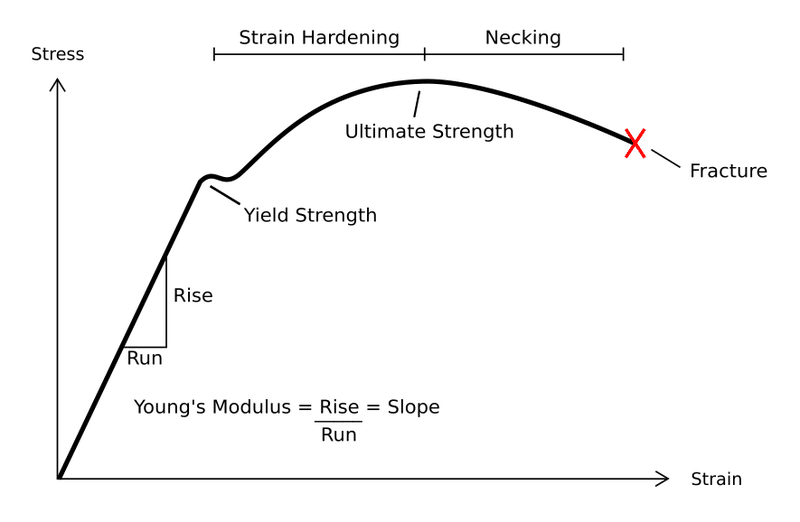
Geometric nonlinearity refers to the changes in shape and geometry that occur when a structure undergoes large deformations. Material nonlinearity considers the nonlinear behavior of materials, such as plasticity, creep, and non-elastic deformation. Contact and frictional nonlinearity account for the interactions between structural components or external objects, including contact forces and sliding friction.
Nonlinear Analysis Techniques
Various techniques are employed in nonlinear analysis to solve the complex mathematical equations involved.
- The Finite Element Method (FEM) is a widely used numerical technique that discretizes the structure into smaller elements to simplify the calculations.
- Additionally, iterative methods such as the Newton-Raphson method and Incremental-iterative techniques are commonly used in nonlinear analysis to solve the nonlinear equations step by step. These techniques divide the analysis into smaller increments and update the solution iteratively until convergence is achieved.
The Finite Element Method (FEM) is particularly effective in handling nonlinear analysis. It divides the structure into finite elements and considers the nonlinear behavior within each element. By assembling these elements, the overall nonlinear response of the structure can be determined.
The Newton-Raphson method is another powerful iterative technique used in nonlinear analysis. It updates the solution by iteratively linearizing the nonlinear equations and solving them until convergence is reached. This method is widely applied in various engineering disciplines due to its efficiency and accuracy.
Challenges in Nonlinear Analysis
Nonlinear analysis presents several challenges due to the inherent complexities involved. One major challenge is the complexity of mathematical models required to accurately represent the nonlinear behavior of structures. Developing these models involves understanding the intricate interactions between geometric, material, and contact nonlinearities.
Another challenge lies in the computational requirements of nonlinear analysis. Since the calculations involve solving nonlinear equations repeatedly, it demands significant computational resources and time. Advanced numerical techniques and powerful computing systems are often required to overcome this challenge.
Convergence issues can also arise during nonlinear analysis. Nonlinear equations may exhibit multiple solutions or diverge during the iteration process. Ensuring convergence and stability of the analysis is crucial to obtain reliable results.
Benefits of Nonlinear Analysis
Despite the challenges, nonlinear analysis offers numerous benefits in understanding and predicting the behavior of structures. One significant advantage is the accurate prediction of structural response under complex loading conditions. Nonlinear analysis considers the effects of large deformations, material nonlinearity, and contact interactions, resulting in more realistic and reliable results.
Nonlinear analysis also enables the assessment of safety and stability of structures. By accounting for nonlinear behavior, engineers can identify potential failure modes, evaluate structural integrity, and make informed decisions to enhance safety measures.
Furthermore, nonlinear analysis plays a vital role in optimizing structural designs. It allows engineers to explore different design alternatives, assess their performance, and identify optimal configurations that meet design requirements while minimizing costs.
Applications of Nonlinear Analysis
Nonlinear analysis finds extensive applications in various engineering disciplines. In structural mechanics, it is crucial for analyzing complex structures, such as bridges, towers, and offshore platforms. Nonlinear analysis is also widely used in civil engineering for studying the behavior of soil-structure interaction, seismic analysis, and assessing the stability of foundations.
In aerospace engineering, nonlinear analysis is essential for understanding the structural response of aircraft components under extreme loads, such as during takeoff, landing, or turbulence. It aids in designing lightweight yet structurally robust aircraft.
Mechanical engineering heavily relies on nonlinear analysis for evaluating the behavior of mechanical systems subjected to large deformations and nonlinear material responses. This includes analyzing mechanisms, evaluating the performance of machine components, and optimizing the design of mechanical systems.
Future Developments in Nonlinear Analysis
As technology continues to advance, nonlinear analysis techniques are expected to evolve and improve. Some potential future developments in this field include:
- Advanced numerical methods: Researchers are continually exploring and developing advanced numerical methods to enhance the accuracy and efficiency of nonlinear analysis. This includes the development of new solution algorithms, adaptive meshing techniques, and higher-order element formulations.
- Integration of artificial intelligence: The integration of artificial intelligence (AI) techniques, such as machine learning and neural networks, can greatly benefit nonlinear analysis. AI can assist in automating the modeling and analysis processes, optimizing the selection of material models, and improving the accuracy of predictions.
- Multi-scale modeling: Nonlinear analysis often involves structures with complex hierarchical materials or heterogeneous compositions. Multi-scale modeling techniques aim to capture the behavior of materials at different length scales, allowing for more accurate predictions of the overall structural response.
These advancements will further enhance the capabilities of nonlinear analysis, enabling engineers to tackle even more complex and challenging problems in various engineering domains.
Conclusion
Nonlinear analysis of structures is a powerful tool that enables engineers to understand and predict the behavior of structures under complex loading conditions. By considering geometric nonlinearity, material nonlinearity, and contact interactions, nonlinear analysis provides more accurate results compared to linear analysis.
Through advanced techniques such as the Finite Element Method and the Newton-Raphson method, engineers can solve the nonlinear equations iteratively and obtain reliable predictions of structural behavior. Despite the challenges involved, nonlinear analysis offers significant benefits, including accurate response prediction, safety assessment, and design optimization.
Nonlinear analysis finds extensive applications in structural mechanics, civil engineering, aerospace engineering, and mechanical engineering. It plays a vital role in analyzing complex structures, evaluating stability, and optimizing designs.
As technology progresses, future developments in nonlinear analysis, such as advanced numerical methods, integration of artificial intelligence, and multi-scale modeling, will further enhance its capabilities and enable engineers to tackle more intricate engineering problems.
FAQs
What is the difference between linear and nonlinear analysis?
Linear analysis assumes structures behave linearly, while nonlinear analysis considers the effects of large deformations, material nonlinearity, and contact interactions.
Why is nonlinear analysis important?
Nonlinear analysis provides a more accurate representation of structural behavior under complex loading conditions, allowing for better safety assessment and design optimization.
What are the challenges in nonlinear analysis?
Challenges include developing complex mathematical models, computational requirements, and convergence issues.
How is nonlinear analysis performed?
Nonlinear analysis techniques such as the Finite Element Method and the Newton-Raphson method are used to solve the nonlinear equations iteratively.
What are the future developments in nonlinear analysis?
Future developments include advanced numerical methods, integration of artificial intelligence, and multi-scale modeling to enhance accuracy and efficiency.


