Becoming section under reinforced section than over reinforced section is good in structural design.
Under reinforced sections shows early warnings adequately before the structural failure. However, over reinforced section will fail suddenly by crushing the concrete.
You may refer to the following article for more information on this concept.
In this article, we are concentration on checking whether the section is under reinforced and the moment capacity of the under reinforced sections.
let’s do it with a worked example.
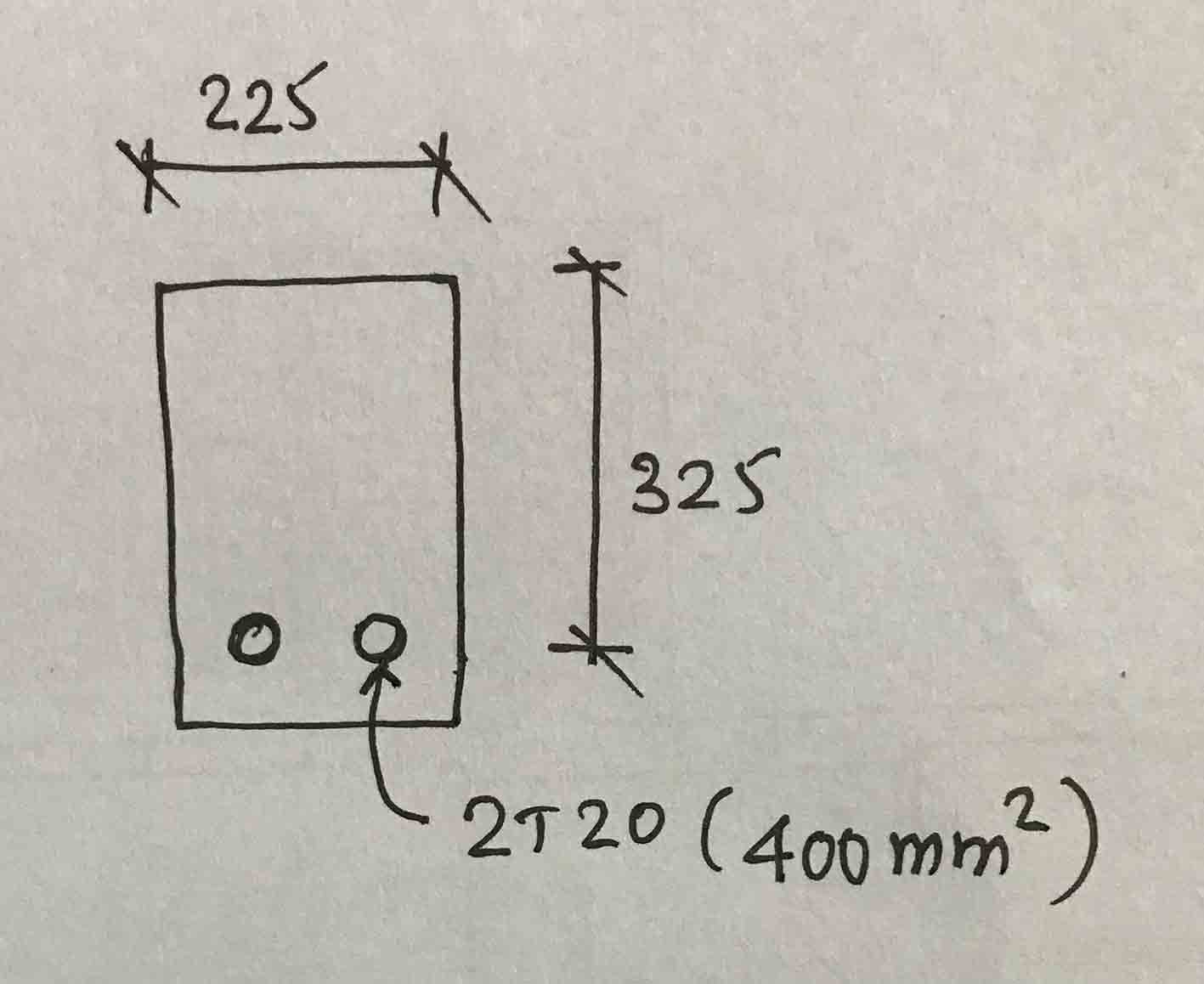
- Single reinforced section
- fcu = 25 N/mm2
- fy = 460 N/mm2
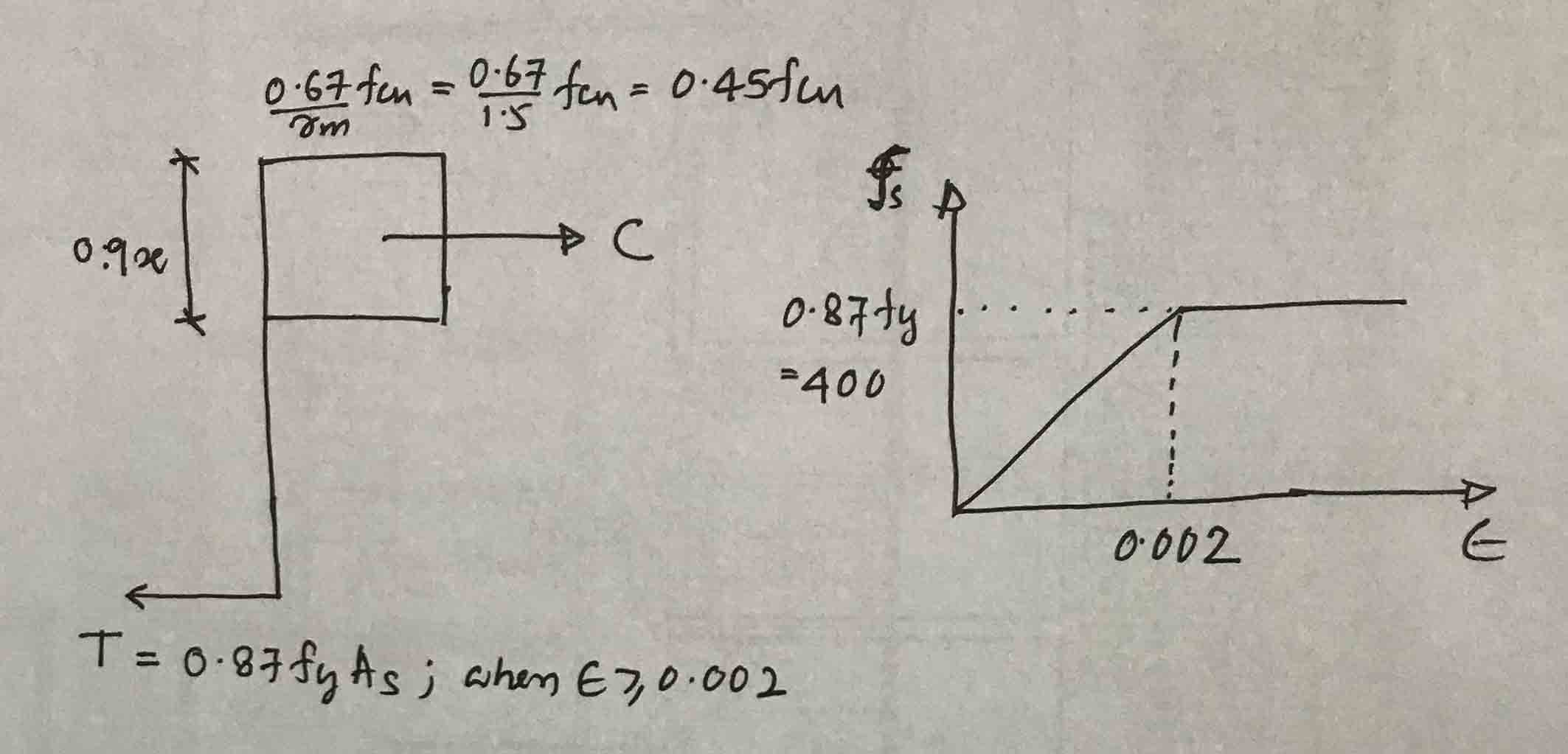
Now consider the stress-strain relationship of the section.
In under reinforced section, steel yielding occurs. If steel is yield, strain is greater than 0.002.
Now, let’s assume steel is yield to calculate the x/d ratio.
T = 0.87fyAs = 0.87 x 460 x 628 = 251325.6 N
C = 0.45fcub(0.9x); where x is the netrual axis depth
C = T
0.45fcub(0.9x) = 251325.6
0.45x25x225x(0.9x) = 251325.6
x = 110.32 mm
x / d = 110.32 / 325 = 0.34
x / d < 0.64 reinforcement yield and assumption is correction.
Therefore, the section is under-reinforced.
Calculate Moment Capacity of the Section
Calculate lever arm.
z = d – 0.45x = 325 – 0.45 x 110.32 = 275.356 mm
z / d = 275.356 / 325 = 0.85 < 0.95
Moment capacity, Mc
Mc = Tz = 251325.6 x 275.356 = 69.2 kNm
The section moment capacity is 69.2 kNm.
Some of the important points worth knowing are listed as follows.
- When the element design are done according to the BS 8110, the x/d value is kept at 0.5 allowing above 10% redistribution of moment in the sturcture.
- When we consider x/d = 0.5, we are in the safe margin and it is required x/d to increase 0.64 to reach the balance condition.
- In addition, as we are well aware, if concrete reaches its maximum strain (0.0035) it will fail suddenly without warnings. when we maintain the x/d = 0.5 in the design, it means, we maintain the concrete strain as 0.002. [x/d = 0.5; d = 2x; if steel strain 0.002, concrete strain becomes 0.002 form geometry]